Benoit B. Mandelbrot
Benoit B. Mandelbrot (1924-2010) was a French American mathematician known as the “father of fractal geometry”. Mandelbrot spent most of his career at Thomas J. Watson Research Center (IBM). He held positions at Yale University, Institute for Advanced Study, and Centre National de la Recherche Scientifique.
Notable Contributions
- Mandelbrot set
- Fractals
- Zipf-Mandelbrot law
Sourced
Mandelbrot, B. B. (1982). The Fractal Geometry of Nature. New York: W. H. Freeman & Company.
Why is geometry often described as “cold” and “dry?” One reason lies in its inability to describe the shape of a cloud, a mountain, a coastline, or a tree. Clouds are not spheres, mountains are not cones, coastlines are not circles, and bark is not smooth, nor does lightning travel in a straight line.
The existence of these patterns challenges us to study those forms that Euclid leaves aside as being “formless,” to investigate the morphology of the “amorphous.” Mathematicians have disdained this challenge, however, and have increasingly chosen to flee from nature by devising theories unrelated to anything we can see or feel.
Mandelbrot, B. B. (1999). A Multifractal Walk Down Wall Street. Scientific American.
The risk-reducing formulas behind portfolio theory rely on a number of demanding and ultimately unfounded premises. First, they suggest that price changes are statistically independent of one another: for example, that today’s price has no influence on the changes between the current price and tomorrow’s. As a result, predictions of future market movements become impossible. The second presumption is that all price changes are distributed in a pattern that conforms to the standard bell curve. The width of the bell shape (as measured by its sigma, or standard deviation) depicts how far price changes diverge from the mean; events at the extremes are considered extremely rare. Typhoons are, in effect, defined out of existence.
Mandelbrot, B. B. (2004). A Theory of Roughness. The Edge.
When you seek some unspecified and hidden property, you don’t want extraneous complexity to interfere. In order to achieve homogeneity, I decided to make the (Brownian) motion end where it had started. The resulting motion biting its own tail created a distinctive new shape I call Brownian cluster. (Figure 1.)
Qualitative properties like the overall behavior of prices, and many quantitative properties as well, can be obtained by using fractals or multifractals at an extraordinarily small cost in assumptions.
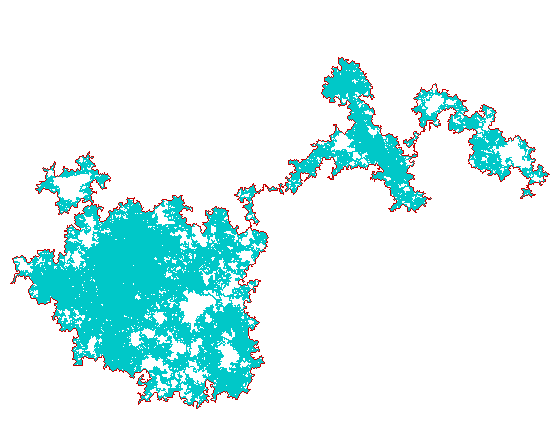
Figure 1 | Brownian Cluster (Source: Alexis Monnerot-Dumaine).
It is beyond belief that we know so little about how people get rich or poor, about how it is they come to dwell in comfort and health or die in penury and disease. Financial markets are the machines in which much of human welfare is decided; yet we know more about how our car engines work than about how our global financial system functions. We lurch from crisis to crisis. In a networked world, mayhem in one market spreads instantaneously to all others—and we have only the vaguest of notions how this happens, or how to regulate it. So limited is our knowledge that we resort, not to science, but to shamans. We place control of the world’s largest economy in the hands of a few elderly men, the central bankers.